Hey there, it looks like you're trying to parse text input in Objective-C. You've come to the right place.
PEGKit is a parser generator implemented in Objective-C. PEGKit converts language grammars into parsers intended for use in Cocoa applications running on iOS or OS X.
With PEGKit, you can define your language with a high-level, easy-to-use, BNF-style grammar, and then generate Objective-C source code which implements a parser for your language.
Specifically, parsers produced by PEGKit are:
- Recursive descent
- Deterministic
- Packrat (or memoizing),
- Backtracking (Infinite-lookahead)
- Predicated
- Written in modern Objective-C (using blocks, ARC, properties)
That's a mouthful, but what it means in practice is that PEGKit offers you a great deal of flexibility and expressive power when designing your grammars, but also produces parsers which exhibit good (linear) performance characteristics at runtime. Also, the Objective-C code produced by PEGKit is clean and readable, and easy to debug or tweak by hand.
The design of PEGKit has been heavily influenced by ANTLR by Terence Parr and a book by Stephen J Metsker. Also, PEGKit depends on TDTemplateEngine for its templating features.
In this tutorial, I'll demonstrate how to use PEGKit to implement a small "MiniMath" expression language in an iOS application. When we're done, we'll be able to parse MiniMath expressions and compute and display the numerical results.
Designing the Grammar
First, let's define for our "MiniMath" language. MiniMath should allow expressions like:
1 // bare numbers
2 + 2 + 42 // addition (including repetition)
2 * (2 + 4) // multiplication and sub-expressions
(2+2)*3 // allow presence or absence of whitespace
3.14 *5 // optional floating point numbers
OK, now that we know what the expected MiniMath input looks like, let's design a PEGKit grammar to match it. Since MiniMath is an expression language, we'll start with an expr rule. But how do we define expr?
expr = ??? // TODO
Rather than designing our grammar from the top down, let's hold that thought, and work from the bottom up instead.
Working from the bottom, we'll start with a rule called atom. And since MiniMath deals with numbers, we'll define atom as a Number.
atom = Number;
Notice how the rules we define ourselves (like expr and atom) start with lowercase letters. There are also built-in terminal rules like Number, Word, QuotedString and more which match common token types like numbers, words, and quoted strings. The built-in rules always start with uppercase letters, while the rules we define ourselves must start with lowercase letters.
The built-in Number rule matches a series of digits as you would expect. By default, it also matches optional floating-point and exponential parts of a number (this behavior is easily configurable, but in this case the default behavior is what we want).
Now that we have defined an atom rule, let's define a primary expression.
primary = atom | '(' expr ')';
A primary expression is either an atom or a parenthesized sub expression. The parentheses will be used to alter operator precedence in our MiniMath language.
Note that we can recursively call our own expr rule (although in PEGKit grammars, you must always avoid left recursion, or rules which point immediately to themselves).
Now let's move on to multiplication and addition. As usual, we want multiplication to bind more tightly than addition. Since we're working from the bottom up, we can make multiplication bind more tightly by defining it first.
Let's define multiplication as a primary expression times a primary expression.
multExpr = primary '*' primary;
But we want to allow repetition in our multiplication expressions, like 2 * 8 * 0, so we'll alter our multExpr rule slightly by wrapping the operator and the right-hand side operand in an optional repetition using *.
multExpr = primary ('*' primary)*;
Our addition rule will look very similar:
addExpr = multExpr ('+' multExpr)*;
Since our addition rule is defined in terms of multiplication operands, this will force multiplication to bind more tightly than addition.
Now we can define our expr rule as an addition expression:
expr = addExpr;
Finally, let's update our grammar to discard unnecessary tokens. The post-fix ! operator can be used to discard a token which is not needed to compute a result. In the case of MiniMath, we'll want to discard any token that is not a number (all of the literal strings in our grammar).
Here's the complete grammar:
expr = addExpr;
addExpr = multExpr ('+'! multExpr)*;
multExpr = primary ('*'! primary)*;
primary = atom | '('! expr ')'!;
atom = Number;
Adding Actions to the Grammar
OK, so we designed a grammar for our MiniMath language that can be fed to PEGKit to produce Objective-C source code for our parser.
But we don't just want to parse input, we also want to compute a result. This can be accomplished in one of two ways:
- Specify a parser delegate object when creating your parser. Your parser delegate will receive callbacks as the parser matches input (like
-parser:didMatchAtom:). - Add grammar actions to your grammar. Grammar actions are small pieces of Objective-C source code embedded directly in a PEGKit grammar.
In this tutorial, we'll use the second option: grammar actions. We'll start by adding an action to the atom rule:
atom = Number
{
PKToken *tok = [self.assembly pop]; // pop the Number token
NSAssert(tok.isNumber, @"a number token just matched in `atom`");
NSNumber *n = @(tok.doubleValue);
[self.assembly push:n]; // push an NSNumber object
};
As you can see, actions are blocks of Objective-C code enclosed in curly braces and placed after any rule reference.
In any action, there is a self.assembly object available (of type PKAssembly) which serves as a stack (via the -push: and -pop instance methods). The assembly's stack contains the most recently parsed tokens (instances of PKToken), and also serves as a place to store your work as you compute the result.
Actions are executed immediately after their preceeding rule matches. So tokens which have recently been matched are available at the top of the assembly's stack.
In this case, we are popping a just-matched number token off the stack, converting it to a double value, and pushing an NSNumber back onto the stack for later use.
Unfortunately, our action code is a bit verbose, and it's making our grammar harder to read and understand. No problem: PEGKit includes some handy macros that can make this code more concise. Here's the atom rule and action rewritten using those macros:
atom = Number {
// pop a token off the stack and push it back as a double value
PUSH_DOUBLE(POP_DOUBLE());
};
This shortened action is exactly equivalent to the more verbose version above. The action still pops a number token off the stack, converts it to a double value, and pushes an NSNumber back onto the stack
Now let's add an action to perform multiplication in the multExpr rule:
multExpr = primary ('*'! primary {
NSNumber *rhs = [self.assembly pop];
NSNumber *lhs = [self.assembly pop];
NSNumber *n = @([lhs doubleValue] * [rhs doubleValue]);
[self.assembly push:n];
})*;
This action executes immediately after the multiply operator (*) and right-hand side primary operand have been matched. Since the * operator has been discarded, we can be assured that the top two objects on the stack are NSNumbers placed by our atom rule action.
Again, we can use PEGKit's handy built-in macros to simplify our Objective-C action code. Here's the same action simplified:
multExpr = primary ('*'! primary {
PUSH_DOUBLE(POP_DOUBLE() * POP_DOUBLE());
})*;
Finally, we'll need a similar action for our addition expression rule. Here's the complete grammar including actions:
expr = addExpr;
addExpr = multExpr ('+'! multExpr {
PUSH_DOUBLE(POP_DOUBLE() + POP_DOUBLE());
})*;
multExpr = primary ('*'! primary {
PUSH_DOUBLE(POP_DOUBLE() * POP_DOUBLE());
})*;
primary = atom | '('! expr ')'!;
atom = Number {
PUSH_DOUBLE(POP_DOUBLE());
};
Interlude: Checkout the Example Project (with PEGKit Dependency)
OK, time to checkout the PEGKit MiniMath Example project. This project includes PEGKit as submodule, and an iOS app target which embeds and links to PEGKit. If you are creating your own app which uses PEGKit, follow these instructions for embedding PEGKit in your app target.
Generating Parser Source Code
Now that our MiniMath grammar is complete, we can use PEGKit to generate Objective-C source code for our parser.
Open the MiniMath Xcode project, then select and run the ParserGenApp target.
ParserGenApp is actually a target in the embedded PEGKit sub-project, and is the way you convert your PEGKit grammars into Objective-C source code.
Paste the MiniMath grammar into the large text area at the bottom of the ParserGenApp window, and select the options shown below.
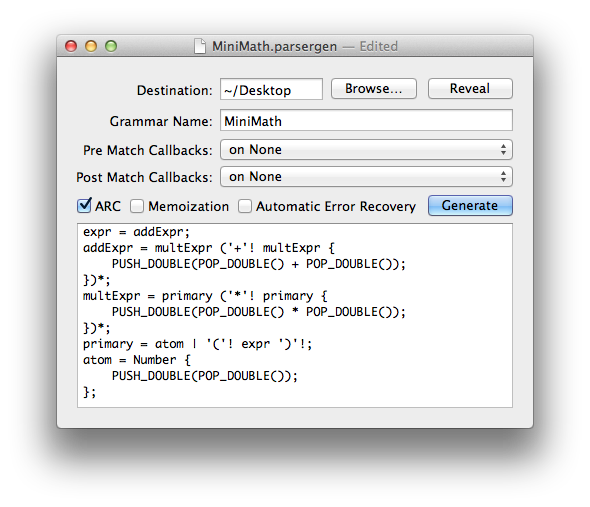
Click the Generate button and notice that MiniMathParser.h and MiniMathParser.m files have been created, and appear on your Desktop. Normally, you'd need to drag these source code files into your app's Xcode project, but in the case of MiniMath, I've included the files already (cooking show style!).

Run the MiniMath Example iOS App
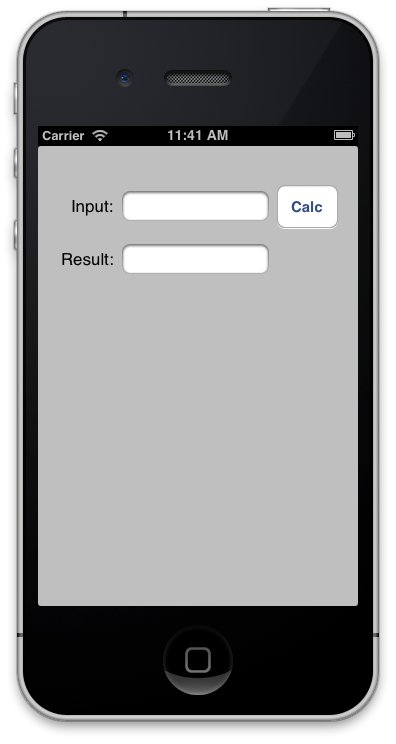
Back in Xcode, switch to the MiniMath target. This target is an example iOS app with an Input textfield, Calc button, and a Result textfield:
Here's the implementation of the -calc: Action attached to the Calc button, showing how to use the MiniMathParser we just created:
- (IBAction)calc:(id)sender {
NSString *input = _inputField.text;
MiniMathParser *parser = [[MiniMathParser alloc] init];
NSError *err = nil;
PKAssembly *result = [parser parseString:input error:&err];
if (!result) {
if (err) NSLog(@"%@", err);
_outputField.text = @"";
return;
}
// print the entire assembly in the result output field
_outputField.text = [result description];
}
Run the app (make sure you've selected the iPhone Simulator as your run destination), and you'll see the input field is pre-populated with an example expression. Click the Calc button to compute and display the result:
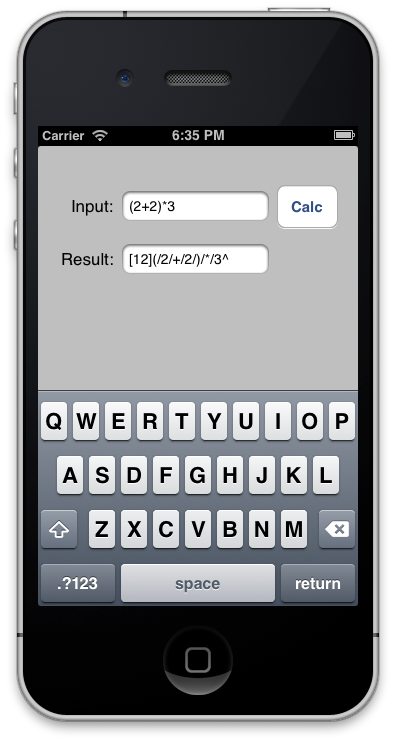
This displayed result deserves a bit of explanation.
The result of the -[MiniMathParser parseString:error:] method is an assembly object of type PKAssembly described earlier. Again, an assembly is intended to be a convenient place to examine recently-matched tokens as well as store temporary work as the parse executes.
A PKAssembly object combines a stack (which we've used earlier in this tutorial) and a buffer of the tokens matched in the input string so far. Printing an assembly via the -[PKAssembly description] method returns a string with the following format:
[ stack, contents, here ] matched / tokens / here ^
The contents of the assembly's stack are on the left between the [ ] square brackets. And the buffered tokenized input is displayed on the right between / slash chars. Each slash separates individual tokens. The ^ caret represents the parser's current cursor position in the input token stream.
So for our result:
[12](/2/+/2/)/*/3^
12 is on the stack. And tokens (, 2, +, 2, ), *, and 3 have been matched. The cursor (^) is positioned at the end of the input string (our parse successfully matched the entire string).
This assembly display can often be useful when debugging parsers. But for now, all we want is the numerical result of parsing our MiniMath expression. As you can see, the result (12), is on the top of the stack. So we can just pop the numerical result off the stack and use it:
PKAssembly *result = [parser parseString:input nil error:nil];
NSNumber *n = [result pop];
NSLog(@"The numerical result is: %@", n);
For our given input of (2+2)*3:
The numerical result is: 12
Conclusion
I hope this simple tutorial will inspire you use PEGKit to parse more interesting languages than MiniMath in your Mac and iOS applications.
To learn more about PEGKit grammar syntax, checkout some of the many example grammars in the PEGKit project.
The main PEGKit repository is here. I'm @iTod on Twitter, and if you find some use for PEGKit, consider checking out some of my other software. Cheers!